一、什么是水仙花数?
水仙花数(Narcissistic number)也称为自恋数或阿姆斯特朗数(Armstrong number),是指一个 n 位数,其各位数字的 n 次方之和等于该数本身。
简单定义:
- 3位数:每个数字的立方和等于这个数本身
- 4位数:每个数字的4次方和等于这个数本身
- n位数:每个数字的n次方和等于这个数本身
二、经典例子
1. 三位数的水仙花数(最常见)
153 = 1³ + 5³ + 3³ = 1 + 125 + 27 = 153 ✅ 370 = 3³ + 7³ + 0³ = 27 + 343 + 0 = 370 ✅ 371 = 3³ + 7³ + 1³ = 27 + 343 + 1 = 371 ✅ 407 = 4³ + 0³ + 7³ = 64 + 0 + 343 = 407 ✅
2. 四位数的水仙花数
1634 = 1⁴ + 6⁴ + 3⁴ + 4⁴ = 1 + 1296 + 81 + 256 = 1634 ✅ 8208 = 8⁴ + 2⁴ + 0⁴ + 8⁴ = 4096 + 16 + 0 + 4096 = 8208 ✅
3. 五位数(很少见)
54748 = 5⁵ + 4⁵ + 7⁵ + 4⁵ + 8⁵ = 3125 + 1024 + 16807 + 1024 + 32768 = 54748 ✅
图形化代码:
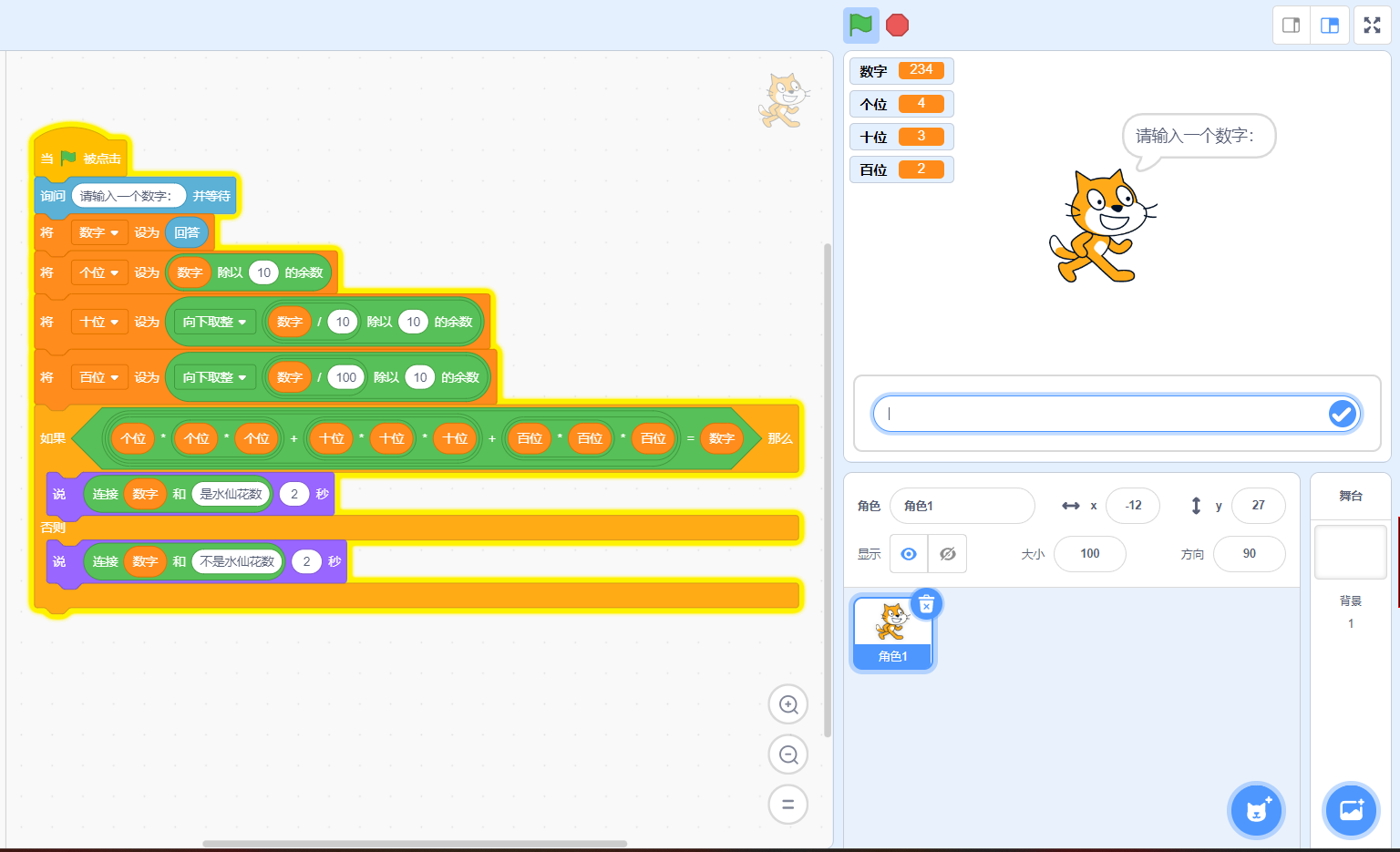
公式 (例如153)
取个位:数字取10的余数 153%10=3
取十位:数字除10取10的余数 153/10%10=5
取百位:数字除100取10的余数(取整数) 153/100%10 = 1
核心定义
奇数和偶数是针对整数(包括正整数、负整数和零)的一种最基本分类。
- 偶数:能被 2 整除的整数。
- 奇数:不能被 2 整除的整数(或者说,被2除后余数为1的整数)。
用数学语言精确表达:
- 一个整数 n 是偶数,当且仅当存在一个整数 k,使得 n=2k。
- 一个整数 n 是奇数,当且仅当存在一个整数 k,使得 n=2k+1(或 n=2k−1)。
图形化代码:
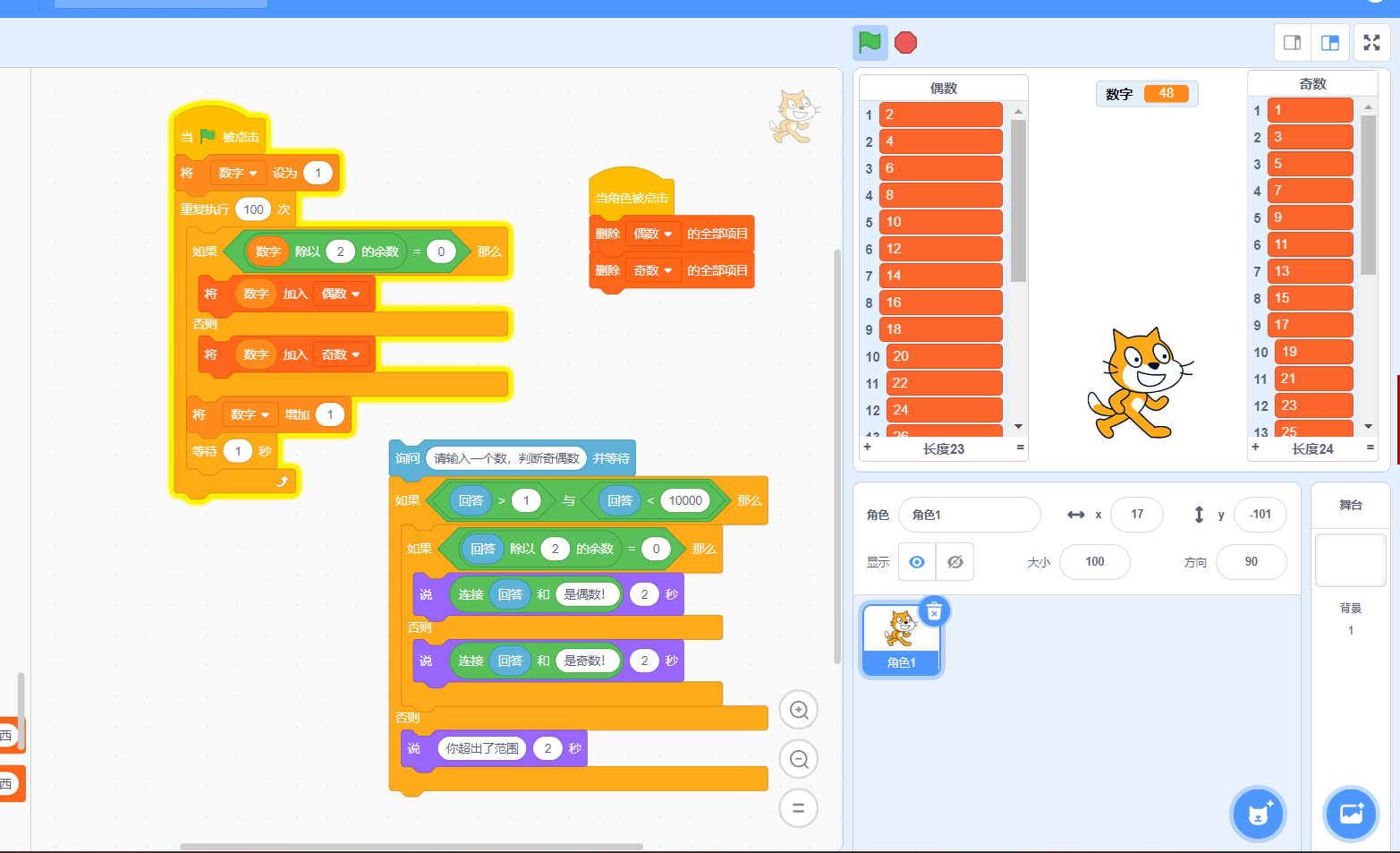
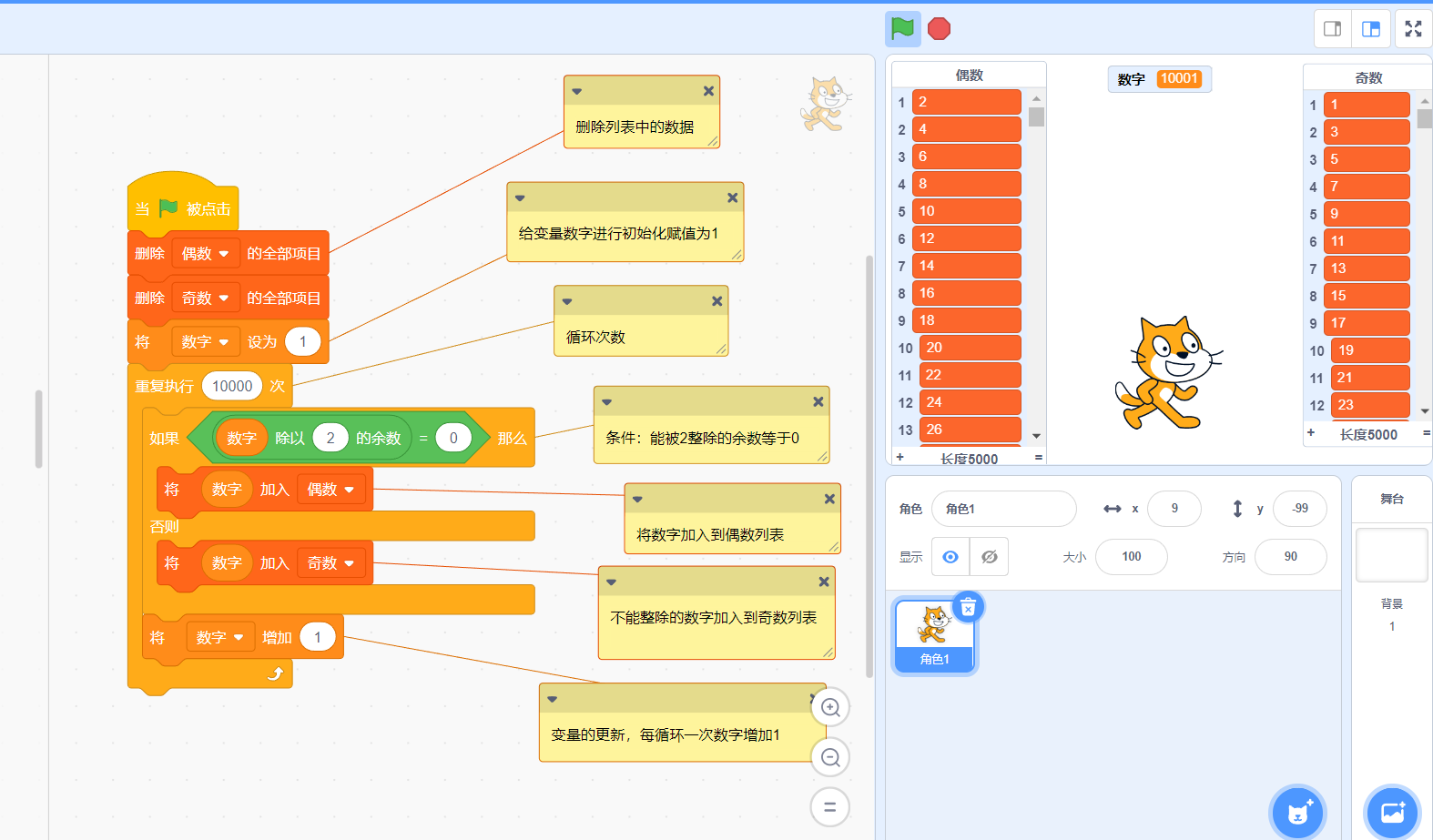
如涉及侵权,请通过邮件:gouweicaosheji#163.com与我联系处理。
 宗宗酱
宗宗酱